Rich and hearty Guinness Beef Stew is a classic that you'll find at pubs and family dinner tables all across Ireland. This version features ultra-tender meat, deep flavors, and Cheddar Herb Dumplings that will make you swoon. It's the ultimate comfort food.
It's been cruelly cold and frosty for the past couple of days up here, which means I had a choice to make. With a forecasted foot of snow on the way, I could either prepare myself to spend a couple of hours struggling to make a dent with my super-sad shoveling skills, or I could cook up a post-snowpocolypse dinner for the guys and try to subtly avoid going out in the cold. Is it even a slight mystery as to what I decided to do?
Ah, my cursed predictability. Yes, I made Guinness Beef Stew with Cheddar Herb Dumplings again.
Since I first published this recipe in 2014, it's grown to be pretty popular-- both on the internet and in my home.
I've made this stew at least a dozen times to get James and I through the winter's chill, and always have enjoyed a bottle or two of the leftover Guinness to reward myself for a job well done. Because at the risk of coming off a bit conceited here, I've gotta say that I'm always proud of myself when I make Guinness Beef Stew with Cheddar Herb Dumplings.
There's something so gratifying about making a dish that's filled with deeply flavorful vegetables, unbelievably tender meat, and an incredibly rich gravy. And when you throw some cheesy dumplings on top, it just gets that much better.
Not to mention it got me out of having to shovel, so that's an accomplishment in its own right. The guys didn't seem to mind at all when there was a big bowl of warm beef stew waiting for them when they came back inside.
But enough about me. Let's get down to business.
WHAT'S IN THE STEW?
LET'S START WITH THE MEAT.
It's not uncommon for stews to feature lamb, especially Irish stews. However, this one features beef. Beef tends to be more accessible for feeding a family as it's less gamy, but you can substitute lamb if you'd prefer.
As far as what cut of beef to use, I always reach for the boneless beef chuck, or chuck roast, as it's also often labelled. There are a two main reasons for this.
- This cut is not a naturally tender cut-- it's a well-worked muscle with a lot of connective tissue. It might seem like that would result in tough meat, but when cooked slowly, as you do in a stew, the connective tissue breaks down, melts, and releases gelatin into the meat, making it moist, rich, and, yes, ultra-tender. Fork tender. Falling apart tender.
- Because it's not an inherently tender cut (as mentioned above) it's actually very inexpensive. There are a lot of ingredients in stew, but none of them should be expensive ingredients. It's more about developing flavor than it is starting with top-of-the-line, expensive stuff.
And we can't forget the bacon. Yes, there's also bacon! Why bother adding bacon to this recipe? Well, it's optional, but we already talked about the beef chuck's connective tissue breaks down and that gelatin keeps the meat moist right?
The thing about that-- the good thing about that, really-- is that it doesn't release a whole ton of fat into the stew. And while we don't want our stew to be swimming in grease, we do want our vegetables to have a great meaty flavor.
By cooking bacon, searing the beef in the rendered fat, and then cooking the onions, carrots, celery, and garlic in the rendered fat as well, you're getting significantly more meaty, deep flavor infused from the get-go.
That being said, you can opt to leave the bacon out and cook in oil or butter if you'd prefer.
HOW ABOUT THE VEGGIES AND AROMATICS?
When it comes to produce, you can get creative, but I try to stick to traditional ingredients. As I mentioned above, I include onions, carrots, celery and garlic, to start.
Onions, carrots, and celery (together known as a mirepoix) are often included in stews, soups, and stocks because they create an aromatic flavor base. Garlic is another aromatic ingredient that will deepen the final flavor of the stew.
Another ingredient I sometimes add for extra flavor is mushrooms-- but they are completely optional.Mushrooms add extra meaty, earthy, savory flavors that make them great for stews, but if you're not a fan, this stew won't suffer without them. In fact, I only include them when cooking for certain people-- my mom and brother love them in this stew, for example, while James and housemate Mike aren't fans of mushrooms so I leave them out.
I also add extra root vegetables for substance, such as potatoes, parsnips, and turnips. I might not use all three, but I do use a lot-- they're great for adding texture and those starchy carbohydrates that balance out all of the meat.
LET'S TALK SAUCE
While soups have broth, a good stew has more of a sauce or gravy-- it's thick, it's comforting, and it's rich. And man, is it delicious.
For this one, you'll need the following ingredients:
- Tomato paste. Tomato paste adds concentrated umami quality, which gives your stew extra savory, almost meaty flavor.
- Guinness beer. Beer adds extra richness and depth, and Guinness is especially great for this!
- Worcestershire sauce. We keep talking about building depth, because that's what stew's about, baby. Worcestershire sauce also lends a tiny bit of tang, too.
- Low sodium chicken broth. Not beef broth?! I know. But chicken broth tends to have better flavor overall, while beef broth can get metallic and lend off-putting flavors. Trust me, you'll get plenty of beefy flavor from the actual beef here.
- Cornstarch. A good stew should be plenty thick, and cornstarch will do the trick. At the very end, adding a slurry with cornstarch will get you to your desired consistency, if your gravy doesn't thicken up fully on its own.
- Herbs. A good stew is seasoned with herbs. This one's got bay leaf, thyme, and is sprinkled with fresh parsley at the end.
HOW ABOUT THOSE DUMPLINGS?
Ah, the dumplings. I'm almost tempted to call them my favorite part, but let's be serious, there's that stew to consider.
The dumplings come together in a flash. Mix together the following ingredients:
- Self-rising flour
- Garlic powder
- Shortening
- Sharp Irish cheddar
- Milk
- Fresh herbs
And dollop them on top of the stew before transferring to the oven to bake.
Once they're browned and cooked through, you're good to dig in.
HOW TO MAKE IT -- THE GUINNESS BEEF STEW VIDEO
MORE IRISH RECIPES TO LOVE
- Irish Baked Potato Soup with Corned Beef and Crispy Leeks
- Dubliner-Dill Skillet Irish Soda Bread
- Malted Guinness Chocolate Cake with Baileys Frosting

Guinness Beef Stew with Cheddar Herb Dumplings
- Total Time: 3 hours 30 minutes
- Yield: 6 servings 1x
Ingredients
For the Stew:
- ¼ pound bacon
- 2 pounds boneless beef chuck, chopped into bite-sized pieces
- Kosher salt and black pepper
- 4 sticks celery, chopped
- 3 large carrots, chopped
- 1 large onion, chopped
- 4 cloves garlic, minced
- 2 large potatoes or parsnips, diced
- 1 turnip, diced
- 3 ounces tomato paste
- 1 (12 ounce) bottle Guinness
- 4 cups low sodium chicken broth
- 2 tablespoons Worcestershire sauce
- 1 bay leaf
- 3 sprigs thyme
- 1 tablespoon cornstarch, or as needed
- ½ pound cremini mushrooms, sliced (optional)
- Chopped parsley
For the Cheddar Herb Dumplings:
- 1 ½ cups self-rising flour
- ½ teaspoon garlic powder
- ⅓ cup shortening
- ¾ cup shredded Irish sharp cheddar
- ⅔ cup milk
- 2 tablespoons mixed fresh herbs such as parsley, chives, and thyme, chopped
Instructions
- Cook the bacon in a large, oven-safe, heavy-based pot or high-walled saute pan over medium heat.
- Remove the bacon, crumble, and set aside, but leave the bacon fat in the pot. Season the beef with salt and pepper and fry in the bacon fat until browned on all sides. Remove the beef from the pan and set aside.
- In the same pot, fry the onion, celery, and carrots until soft and fragrant, adding a little oil if necessary.
- Add garlic and fry for another 30 seconds. Stir in the tomato paste.
- Pour in the Guinness and Worcestershire sauce. Allow to come to a simmer and stir with a wooden spoon, scraping up the browned bits from the bottom of the pot.
- Add the beef back to the pot and pour in the chicken broth. Add the bay leaf and thyme.
- Reduce to a simmer and cover. Simmer for 1 ½ hours. Add the potatoes or parsnips and the turnip. Simmer for another ½ hour, or until the vegetables are tender.
- Remove the bay leaf and thyme branches. If the stew is still thin, mix a tablespoon of cornstarch with a tablespoon of cold water to form a slurry. Mix the slurry into the stew and bring the mixture to a boil. Reduce to a simmer again, stirring occasionally, and add in the mushrooms if desired. Cook for 10 minutes, uncovered, until the stew thickens and the mushrooms are cooked through. Stir the bacon back in. Preheat the oven to 350°F.
- Stir together the self-rising flour and garlic powder in a medium bowl. Cut in the shortening until mixture resembles coarse crumbs. Stir in the cheddar cheese, then add the milk and stir until the dry ingredients are moistened.
- Make small balls with the dough and place them on top of the stew, leaving them room to expand-- they grow a lot as they cook. Place the stew in the oven uncovered and bake until the dumplings are browned and cooked through, about 30 to 40 minutes.
- Garnish the stew with parsley and serve.
- Prep Time: 30 mins
- Cook Time: 3 hours











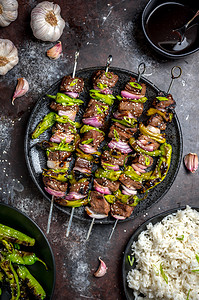


Jason says
Hi,
For the Guinness beef stew. Is the bacon supposed to go back into the stew at some point or is it just for it's grease.
Thanks, and Happy Holidays!
Jason
Morgan says
You can add the bacon in at any point if you like, for extra flavor, but you don't have to. I believe I just used it for the grease and ate the bacon separately (can't resist, haha). I hope you have a very happy holiday as well!
Berly says
I'm going to put the bacon in the dumplings, yum!!!
Stephi says
See step 8
T says
Never thought to put the bacon in the dumplings. Great Idea!
Dawn Fulton says
Reread step 8 in the recipe. There's you answer
kate says
are the carrots supposed to be added in step 3 or step 7 cause they are listed in both?
Morgan says
Woops, step 3! I will fix that as soon as I get a chance.
Tevin says
Hi there! Looks so great, making this tonight but only have potatoes to sub for parsnips and turnips. Hope it turns out as good as it looks! 🙂
Corinna says
Yum!! Making this for book club!! About how many servings does this make?
Morgan says
This stew makes 4-6 servings. I hope your book club enjoys it!
Nicole H says
What size pot did you use? Thinking I need to make a double batch and want to make sure my pot is big enough.
Morgan says
I believe that's an 11" high-walled skillet.
maria says
you didn't say when to re-add the bacon
Dawn Fulton says
Yes she did. See step 8
Timing Matters says
90 minutes for first simmer, add veg then 30 min, plus 10 for mushrooms, plus 25 min for the dumplings equals 2:35 of cooking time, not 1:45. Ended up eating dinner really late. 🙁
Morgan says
I'm so sorry for that! I believe I meant to write "2:45" and it was a typo that I somehow didn't catch! Again, I'm so sorry about that.
Timing Matters says
It's OK! You've fixed the timings and I've had delicious leftovers. 🙂
Nicole H says
I made a double batch yesterday!! Amazing!! Definitely a challenge for me, as I have never dealt with dumplings, parsnips, or turnips before!
So much fun and so delicious!!
We made mash potatoes to go along with, a 3:1 ratio regular potatoes to sweet potatoes! Amazing!
Wish I could post pics, but you can see them here: https://www.facebook.com/photo.php?fbid=10103382401876560&id=23900451&set=a.10101347683253990.2764682.23900451&source=43
Kim says
I would just like to say that this is the MOST DELICIOUS stew I have ever made, and for years I've tried many variations. Yes, it takes time, but it isn't hard, and is totally worth it! The broth has such a richness, and the dumplings make it. Thanks so much for this wonderful recipe!
Erin says
How many stews have you made in your life?
Stephan says
Do you think I can make this in my enamel Dutch oven? I'm not sure how the time would be affected though!
Nicole says
I made mine in Le Creuset Dutch oven. It was perfect!
Stephanie says
I'm going to cook this tonight - I've done all of the chopping already! I was surprised to learn that it is only 3-4 hours in the crock pot though, as I've made similar recipes and they've been closer to the 7-9 hour range. Does this mean that I should put it on my highest setting on the crock pot? Thanks!!
Morgan says
Hi Stephanie! This is not a crock pot recipe, it's just made in a pot on the stove. I'm sorry for the confusion!
Melodie says
Could you specify which herbs were used for the cheddar dumplings? Looks delish
Gail says
I want to make this for St. Patrick’s Day party. Want to make in my crock pot. I’m assuming I could just cook for 6-7 hrs. On low and add mushrooms at the end. I plan to bake dumplings as biscuits. Hope it works - sounds wonderful!
Alexandra Timmons says
Did you try in crock pot?
Amaryllis @ thetastyother.com says
This must be the most delicious recipe I've seen in awhile! I absolutely love everything about the stew and can't get over those cheddar dumplings! Thanks for sharing, Morgan!
Rachel says
I made this tonight. I got a tad confused by the recipe, as I was instructed to add the carrots twice and the bacon was "set aside" and never brought up again. I ended up adding the carrots in the beginning and throwing the bacon in when I added the beef back in. Regardless, the stew was deep with flavor and my family couldn't get enough. I do recommend adding a bit of salt, but that's really the only modification I made. It wasn't very thick but we left it that way and thoroughly enjoyed it. Thank you so much for sharing this delicious recipe! I will definitely make it again!
Valerie says
This stew looks amazing! I will have to try this recipe soon. The dumplings look delicious I can't wait to try them.
I have a hearty beef stew that I usually make but it might be time for a new recipe. 🙂 http://doubletherecipe.com/2016/03/02/hearty-beef-stew/
Thanks for sharing.
Ashley says
Hi! Should I cut up the beef or leave it as a whole roast?
Cat says
You must be new to stew? It is always cut up into chunks .... this recipe states bite size chunks.
Christina says
I am currently on lockdown from our social distancing protocols and I didnt have access to guiness, so I used a 1/2 cup of coffee and a tablespoon of sugar instead. It turned out beautifully. Loved this recipe! Thank you for sharing.
Richard says
What do you consider "mixed fresh herbs" for the Cheddar Herb Dumplings for the Guinness Beef Stew?
Morgan says
It's up to your preference: parsley, thyme, rosemary, and chives would all be good options!
Beverly Hart says
I don't really like the taste of beer. Is it a very pronounce flavor? Or more for tenderizing?
Bethany Ford says
I used this recipe as the guide for a vegetarian version. It was amazing! The biscuits needed just a few minutes under the broiler at the end to get a crisp golden top. Really delicious!
Lori says
Can you tell me how you modified this for a vegetarian version?
Alyssa Serra says
Yes please!
Shauna Harrison says
Did you just do butter instead of the bacon & double the vegetables added?
Jennifer says
How many servings does this recipe make? And, is it possible to make the dumplings separate from the stew and add them in individual bowls? (I'm thinking of making a double recipe, but figure there wouldn't be space in the pot for double the dumplings.)
Evelyn says
Do you think using the Box with directions of Red Lobster biscuits work for the dumplings? And then possibly placing my La Creuset in the oven and boil the top to make the tops brown and crisp? Or make the biscuits separately and top each individual serving with it?
Julie says
I made this for our dinner. We haven't actually eaten, because my husband isn't home from work yet, but boy does our house smell amazing!! I can't wait to dig in! I found the recipe very simple to follow, and even added a handful of cooked quinoa to it, as well. Thank you for sharing it!
OregonGirl says
I was really looking forward to making this recipe because it looked so good. I ended up not liking it at all but the friend I had over for dinner loved it and said it was the best stew she'd ever had. She did say that she doesn't normally like stew and I do so maybe that says something. I thought it tasted sort of like cinnamon and I didn't use any. I followed the recipe exactly. My husband didn't like it either. The stew and dumplings turned out fine so the recipe was accurate we just didn't like the taste.
Morgan says
Sorry to hear that! I can't think of why this could possibly taste like cinnamon, though! Do you normally like the taste of Guinness? Perhaps that's where it went awry?
Cristina says
Hi there. Any suggestions on how to make this in the crockpot? I would love to make this for St Patty's Day but will be away for a baseball game most of the day a few hours away
Jan Mowbray says
I intend to use this recipe to serve 120 people (mostly Seniors) for a Celtic dinner on Mar 24...when one starts multiplying out that far, quantities are critical. The recipe says it serves 6, though I seem to recall it's something less in one of your replies above. Can you tell me if the 6 the recipe says it serves are 6 generous servings? We will be serving it with a side Colcannon as well as Soda Bread biscuits - a lot of carbs I know but it suits our clientele.
Morgan says
Hi Jan, yes it makes 6 filling servings! However I'd definitely recommend testing a gently scaled-up version first to get a feel for your quantities and how you might have to adapt to make that large of a batch. I think it sounds like a delicious dinner!
Sarah says
This was super good! I made it last night. Maybe it was the type of potatoes I got, but it took a lot longer to cook them. I bought Yukon gold instead of Idaho. But man, everyone was impressed with it! Thanks.
anjalee says
This looks so yummy! I'm not allowed to cook with alcohol or bacon though. If I removed them would it still taste flavorsome? Will I need to adjust the quantities of the other ingredients to make up for it?
Morgan says
It will be fine, Anjalee, just use butter instead of bacon grease and additional chicken broth instead of the beer. =) You might want to make some slight adjustments to taste (like perhaps more Worcestershire sauce for more depth of flavor) but otherwise you'll be all good!
Laura says
I don't have crisco. What else can I use
Shawn Marie says
I made this today this was absolutely delicious the biscuits were so yummy. I put the bacon in the biscuits instead of in to the stew. I will definitely be making this again.
Annisa says
Hi, I was looking for this answer too! Did you by chance end up using butter? Did it work? Thanks 🙂
Substitutions-r-Us says
Do you have Bisquik? I'm thinking you could make biscuits with it instead, and just spike them up with the shredded cheddar?
Macie says
We just got back from Ireland and were missing a good Irish meal! This was SO good. I made it for my husband and parents and I will definitely be making it again -- it was a hit! I didn't add the mushrooms this time since my husband isn't a fan of them, but I'm definitely going to try it next time and he can just pick them out 🙂
Christin says
Im planning on making this over the weekend, saw one person put the bacon in the dumplings which sounds amazing.. do you suggest a combination of chicken and beef broth, and have u ever tried it with a lil rice added in???
Lisa says
DELICIOUS ! USED PARSNIPS - DIDN'T MISS THE POTATOES AT ALL!
Opted not to make dumplings and served with fresh crusty italian bread -
had to add an extra tablespoon of cornstarch slurry to get stew constancy without
the dumplings.
Natali says
Just made this tonight I added a half a cup of cabbage at the potato stage cuz I love it in beef stew .i will definitely be making this again!
Shannon says
This came out great! Just looked back at the title and realized the herbs were likely supposed to be added to the dumplings but I don't see that anywhere in the recipe. Did I miss something? Thanks!
Paula says
So tasty! Mine looked just like the picture. It is totally worth the effort!
Vickie Hamann says
Hi-
This is a wonderful meal. I did not have Guinness in the house and it was a snow storm so I gave it a whirl anyway. I am sure the bacon really had something special to do with this recipe. It was excellent I cannot wait to try it with the beer. The perfect meal to make on a snowy weekend. Thank you so much for your website.
Sherry Duin says
So good, is really an understatement...Worth the cost of the expensive Irish cheddar and the 3+ hours. Yum! Yum! Yum! Husband and son both taking in lunch tomorrow. Those dumplings are so yummy, I wanted to eat them all. The meat was so tender. The flavor the Guinness gives it is a deep rich flavor. Thanks for sharing! Officially a fam fav!
Annie says
This recipe is soooo good!!! I don’t even care much for beef or beer but I initially tried this because my husband said it looked good and I thought, okay, I’ll try it. It’s so amazing, has such a depth of flavor, I had to make it again! It’s simmering away right now and I can’t wait for dinner tonight!
I put a rutabagain with the parsnip and turnip - gotta love those root vegetables!
Thank you for putting this out there!
Bob says
Made it tonight. Delicious. . It did take quite a while. But worth it. The directions could be a tad clearer... I wasn’t sure when to add the herbs to the biscuit dough. Couldn’t taste the cheese at all in the biscuits. But still good.
Michelle says
Noticed the same lack of clarity in the instructions for when to add the herbs, however it is included in the video/gif.
Diane says
Definelty a keeper, yum!
Stacey says
Huge hit!! Everyone loved it. Doubled the recipe which was a good thing as several went back fir seconds and thirds!!!!!
Teri vrable says
I have no self rising flour. Is there a way I can substitute?
Morgan says
Yes! For every cup of self-rising flour, you can replace it with 1 cup of all purpose flour, 1 1/2 teaspoons of baking powder, and 1/2 teaspoon of salt.
Amy says
It's a grey, dreary fall Sunday and I'ce got this simmering on the stove. It smells amazing! Can't wait to dig in!
Brandy says
This was great! I’m saving this recipe for sure. I used elk instead of beef because we have that aplenty. The only thing I think I will add next time is something to give it a little heat, maybe some cayenne. The dumplings are amazing! Thanks so much.
Renee Matarese says
Absolutely delicious! I couldn't find a turnip ANYWHERE so I added both the potato and parsnips. I made my own, homemade broth which always makes a difference too. What a great weekend meal for a chilly day.
Karen says
I made this last weekend for my meat and potatoes (and few veggies) man. He devoured it. Thanks!! We're having a progressive dinner on Saturday and I'd like to make this again, but due to time constraints, I want to make the stew in the crock pot and make a pan of rolls earlier in the day. Do you think it would work in the crock pot if I put it in early enough?
Morgan says
I haven't tried it in the slow cooker but I think it would work well!
Alex says
Hi there I would love to make this for st paddy’s day dinner party in a few weeks based on the amazing reviews. Lots of people have asked about slow
cooker adaptation and I wonder if you / anyone could advise timings for low setting? Also, what potatoes do you use? Waxy or floury? Thanks so much in advance
Amy says
This looks fabulous! I’m planning on making it over the holidays. Do you think I’d be able to make the biscuit dough ahead (up to the point of adding the wet ingredients)? I’d like to have it ready ahead of time and be able to toss it in the oven while enjoying a cocktail with family! Thanks!
Morgan says
Yes that would be fine, Amy!
Savanna says
Super excited to try this recipe this weekend! However I am gluten free, do you have any suggestions on how to substitute the flour to make gluten free dumplings ? Thanks!
K says
Hi! So I’m not really a cook -(and I don’t cook meat!) but I want to make this for my boyfriend. Don’t laugh - but is shortening just Crisco? Can I use something besides Crisco?
Signed,
Domestically challenged
Thanks!
Linda says
Made this yesterday for St. Paddys day and it was excellent. Even was well liked by my finicky cousin who went back for seconds. Will make it again for sure. Will worth the prep time!
Rebecca says
Unexpectedly fabulous, though time-consuming to prepare.
Lisa Y says
This is one of the best recipes I have ever made (and I cook A LOT)! My kids and husband love it! I have made this three times in three weeks now. Not only do they love it as dinner but they fight over the leftovers for lunch. It is time-consuming but worth the time for how delicious it comes out!
Katie says
Do you have any suggestions on the meat - I have an issue where it’s coming out “chewy”. Otherwise the flavoring is amazing! What am I doing wrong on the meat?
Trevor says
This is hands down the best stew I’ve ever made, and I’ve made it several times in the last few years. I like to double the recipe and slow cook it in the crock pot. I like to add a little bit of chili flakes, just enough to give it a slight bite. I also like to put in some frozen peas at the end to help cool/thicken/color it up. If I make the dumplings with it, I just put the pot in the oven. It’s a crowd/potluck favorite!
Maria says
Do you mean you made it in the slow cooker and when it was done added the dumpling dough and finished it in the oven? How long did it take to finish in the oven? Thanks for your help.
Alexandra Timmons says
Hi! Please can you advise on timings for crock pot - how many hours low or high and at what stage etc. I will also be doubling for a dinner party. Thanks!
Alexandra Timmons says
How long on low can you advise? Cooking tomorrow!
Sherry says
I made this tonight and boy was it a hit! Both teen daughters devoured theirs and my husband ate 3 bowls with 3 biscuits! I will definitely be making it again! I've already sang praises about it and shared the recipe with three of my foodie friends so far, I'm sure I will think of a few more to rave to about it and share with. Thank you Morgan for giving us this fantastic recipe!
Chris says
This looks delicious. Can the stew be made in advance and frozen?
sheryl says
well, it's cooking, don't know if i'll get an answer before it's done,, but the only alt and pepper is on the meat? is this correct or am i missing where to add more? i hate to have spent all this time and not enough flavor, at what point do i tast and adjust seasoning? help!
John M says
Can you make yhe dumplings an hour or so before its done. Want to clean up before the misses gets home
Summer Yule says
Delicious! The only substitution that I made is that I used lard in place of the shortening for the biscuits. This one is more of a weekend meal time-wise but it made enough to cover my family for an additional dinner later in the week. Loved it, 5-stars!!!
KH says
can this be made in the slow cooker
Pickles says
Absolutely amazing, and received rave reviews.
I used dried herbs instead of fresh in the dumplings to save money, and they were still fabulous.
Morgan says
I'm so glad you liked the stew!
Tim says
Made it last night and my family completely devoured it. Great comfort food. Adding the mushrooms late was a great idea, and really gave the stew some depth.
Steve Thompson says
This is going to be my permanent recipe for winter . I have made many stews and casseroles in the past but this is an absolute favourite with those wonderful dumplings , and all the ingredients are perfect . Thank you very much .
Mr. Guy says
Found your recipe after it was posted on Reddit. Amazing recipe and thank you for the detail about why you do some of the steps the way you do.
I have one gripe however, please don't put bogus prep times. There is no way anyone could knock out the prep in 30 minutes. There are far too many ingredients that require washing, slicing, chopping, dicing, mincing, etc.
I have to say, your blog is great but what's with the dishonest prep time? Do you think somebody is going to stop reading your blog if the prep times are realistic? On the contrary, I probably won't be back to your site because of the aforementioned inaccuracy.
Thanks for the great stew though.
Toni-Marie says
Hi Mr Guy,
My prep time was just under 30 minutes. I count prep time as peeling, cutting, prepping the veggies, cheese, meat, measuring spices, basically having most ingredients ready in bowls to add and cook when the time comes.
Cook time starts the moment I turn on the stove and add food to cook.
For me the timing posted was accurate. Depending on how large the stew is and what ingredients I add prep takes me 20 to 35 minutes. We all peel, dice and slice at different speeds, definitely not a reason to stop reading a blog and miss out on good food ideas.
The final result is absolutely fabulous, a very comforting, hearty meal. Everyone who ate the stew raved about it and had 2 or 3 helpings.
Now my go-to stew recipe. Using bacon in a stew is a game changer, why didn't I think to add it years ago?
The dumplings are to die for, cheese is the secret ingredient!!! I tried a sharp smoked cheese in the last batch, very tasty.
I needed to figure out the ratio of baking soda and salt to use when substituting regular flour for self rising.
A quick Google search and viola! Plus I noticed the answer in the comments today when I finally decided to thank Morgan for sharing this delicious dish.
This is how I found your post, questioning the prep time, and posting a favourable review about the recipe itself.
Best thing about cooking a stew is you adjust ingredients based on what you have on hand in your pantry and the flavours your family enjoy eating, very versatile meal.
Morgan, thank you for sharing this delightful stew recipe. Didn't know you had a blog, will take a look at it to see if I find another tasty treasure.
Toni
Susan T. says
Phenomenal flavor. I can't say enough about this recipe. I couldn't find Irish sharp but found another strong Irish cheese to use and wasn't disappointed. Leftovers for dinner tomorrow!!
kelly says
Why do you use chicken broth instead of beef broth?
Kevin559 says
I'm making this for dinner tonight. In fact, I just put it in the oven with the dumplings for the final stretch.
I substituted venison for beef and no matter how it turns out I won't hate because I can look at the ingredients and know that this is a great recipe.
Crossing my fingers that the venison is tender.
Lisa KK says
I've been making this stew for the past 5 years and it has never failed to be a pleaser. Just came back to get the recipe again and wanted to say thank you for this delicious stew!
Thomas says
What oven temperature should be used? It's not listed.
Morgan says
It's in step 8-- 350F 🙂
Saundra Shaw says
The stew was amazing and I love Irish Stew! I had to use an IPA and a little red wine as I was out of Guinness and it was too cold a day to justify a trip to the liquor store! I baked the biscuits separate so we could add them all week. They were okay, but the stew is the showstopper! I made my slurry with red wine and cornstarch to thicken. Adding the bacon and simmering for awhile enhanced the flavor. Thanks for this great recipe and the tip on making self rising flour. And, Mr. Guy should just settle down and enjoy the process. Good things come to those who wait!
Tina says
This was an amazing recipe! Followed directions but my gravy reduced down really quick. So, I had to add more Chicken Broth. I would have to add my potatoes prior to directions in recipe as they were not done at the duration indicated to put in oven.
Christina king says
Seriously good. I added this to my favorites.
Juliebell says
I am making this over the weekend. Can butter be subbed for Crisco? Thanks in advance.
Emily says
Hi! This looks wonderful. Can't wait to make it for Valentine's Day this year!
Is there a way to make the biscuits without shortening?
Wine lady says
Made this tonight and it is the best stew I have ever made. This was my first time using parsnips and turnips. I liked them better than potatoes.
The dumplings were excellent and easy. One note I will add. I did not have self rising flour. I only had all purpose. I added 1 1/2 tsp baking powder and 1/4 tsp. Salt to flour and they turned out perfect.
We enjoyed dinner wi5h a Zinfandel from Paso Robles California
Jessica says
I’ve made this recipe a few times now but just last night finally made with parsnips instead of potatoes- GAME CHANGER. Always a hit
Amand says
Do you have to use self rising flour?
Sandy says
This looks delicious and I plan to use dry herbs. As I don't have. Fresh ones in the house. Hopefully the dumli gs will turn out well.
Sinno says
Happy St. Patricks Day!
Just made this, it was great! I usually doctor stews and was initially sceptical of the recipe using chicken stock rather than beef but the broth is wonderfully rich and perfectly balanced, didn't change a thing, loved it!
Tamar says
As everyone else has said an absolutely delicious stew. The family devoured and we will definitely be making it again.
Amanda says
Made this recipe, and it by far beats other Guinness beef stew at hay I’ve made. Recipe is great. Family loved it and I’ll will definitely make this again. Thanks for sharing.
REBECCA says
I can’t wait for a cold day to make this (Florida), so I’ll be turning the a/c down and diving into this amazing recipe. I’ll be using a slow cooker for the majority of the cooking, then was going to put in a Dutch oven for the last bit with the dumplings. Any suggestions?
Christine says
Made this for my niece. I added sweet potatoes, swede and a parsnip
For the dumplings I added cheddar and Parmesan, I loved it I don’t usually like dumplings but they were so melt in your mouth delicious
I’m glad I have another recipe to add to my winter warmer menu
Love love love this, I definitely would recommend
Kathy B says
My new favorite stew recipe! I was too lazy this time to make the dumplings, but I will next tome.
Jennie says
I never comment on recipes but this one is too good not to send some love. I made it on a whim and it's a regular in my rotation now. It takes some time but it's so worth it. I think it's a pretty forgiving recipe, last time I only had 1 tbsp of worcestershire and it still came out fantastic. I've just spent a couple hundred bucks on a massive dutch oven so I can double the recipe. Seriously you need to make this.
Kate says
Made this with with venison instead of beef and it was wonderful! Perfect comfort food to get my family and I through the cold snap
Kelli says
Seriously great recipe! I used a Scottish ale since I didn’t have Guinness and it was a major hit. I’ll definitely make this again.
Tammy says
I'm not sure if I have already left a review or not but this recipe deserves it! It was by far my husband and I favorite stew recipe! I keep telling my friends to make it because it is sooo delicious and hearty. Like other reviews, I usually am not a huge fan of stews but I always make them hoping that I can start liking stew because of all the veggies. I am here to say, I am now a huge fan of stew but only this one.
Recipe sounds a little difficult but it really isn't once you get started.
Lara says
I didn't make the dumplings but the stew was great! (Used potatoes only because it's what I had on hand.) Easy to make, beef was tender by 2.5 hours. Good stuff!
Deb says
Great recipe and it made plenty to have for leftovers as well. I used a food processor for most of the prep work and that helped. Thanks, will make this again!
Suzanne says
This looks so good! What a great lunch for the weekend!
Vanessa says
Thanks for sharing! Does it keep long?
N says
Can you use beef stock instead of chicken?
Morgan says
Yes you can!
Ann says
Delicious recipe! I want to make it for a friend for a “meal train” meal so would be making it ahead of time for them to re-heat. How would handle the re-heat and also the dumplings? TIA!!
R. S. says
Great recipe! New family fave. I wish the ads didn't print with the recipe though. It makes for an annoying number of pages to print out and it's difficult to view the ingredients and instructions in an efficient way when there are so many pages to flip thru.
Tammy Williams Willhard says
Suggestions for reheating leftover?
Back pack nana says
Just made this in an instant pot, have to adjust liquid a bit. I used just 2cups of VEGETABLE stock as I didn’t have chicken, but all the Guinness.So timing, 40 mins after sautéing carrots celery & onion, then 10 minutes after adding root veg. I then plut the dumplings in and put the lot in the oven so they’d be like the original. Of course you could just bring the whole thing back to pressure with the dumplings in, and that’s it, as soon as it reaches pressure turn it off. FAB
Stephany Harvey says
This is the best stew I’ve ever made. Thank you sooooo much! I use a Nesco pressure cooker, and all fresh veggies. I even had some long beans I had cooked the day before, and subbed them for potatoes. I used a Czech Pilsner, and I used cheddar cheese spread in the biscuits. We are only two, so we made a small stew, and now I wish I had more.
Morgan says
I'm so happy to hear that you enjoyed the stew, Stephany!!
Kimberly says
This was excellent! Used a bit more bacon and beef than it calls for, but otherwise made to the recipe. The flavor is so rich and perfect for the fall that I so desire to approach. Thank you for sharing your recipe, our family truly enjoyed it.
Morgan says
I'm so glad to hear it Kimberly! And I'm so ready for Fall too!!
Jen F says
I can’t even describe how delicious this was. It will become a part of my regular fall/winter rotation.
Lisa says
A delicious stew! I improvised a few dry herb ingredients based on what I had on hand. Omitted parsnips and turnips, and because I had fresh sourdough bread, and served in bread bowls instead. Looking forward to making this again with the biscuits. This recipe will go on regular rotation this winter. Thanks!
Morgan says
Fresh sourdough bread bowls sound just as fantastic, Lisa!! I'm so glad you enjoyed it!
Kelly says
I loved this stew, and have made it several times.
Question, could you make this with brisket instead of chuck?